碰撞检测
在许多的动画与绝大多数游戏中,都会应用各种形式的碰撞检测,本文主要记录碰撞检测的原理以及应用实现。如何检测两个图形之间是否发生了碰撞,有的检测比较简单,比如矩形与矩形之间的碰撞,圆形与圆形之间的碰撞,有的一些检测方式稍微复杂,例如多边形之间的碰撞,不同图形之间的碰撞,不规则图形之间的碰撞,图形在三维空间中的碰撞。比较常见的碰撞检测方法有 —— 外接图形判别法 / 光线投射法 / 分离轴定理。
外接图形判别法
一般在二维平面中碰撞检测,通常是根据物体平面是否发生重合来判定。对于不规则的物体,其实都可以抽象为一个矩形或者圆形, 然后根据物体的外接矩形或者外接圆形来判定,外接图形判定方式比较简单。外接图形会被当作物体的轮廓来参与碰撞检测,此时也被称作为 “边界框” (Bounding box), 通过检测两个轮廓是否有相交来判定。
外接矩形判别
判断两个矩形是否碰撞,只需要检查一个矩形各个边是否在另一个矩形内部。
1
2
3
4
5
6
7
8
9
10
11
12
| const isCollided = (sprite, detectSprite) => {
const spriteRight = sprite.left + sprite.width;
const detectSpriteRight = detectSprite.left + detectSprite.width;
const spriteBottom = sprite.top + sprite.height;
const detectSpriteBottom = detectSprite.top + detectSprite.height;
return (
spriteRight > detectSprite.left &&
sprite.left < detectSpriteRight &&
spriteBottom < detectSprite.top &&
detectSpriteBottom > detectSprite.top &&
)
}
|
外接圆形判别
判断两个圆形是否碰撞,只需利用勾股定理要检查两个圆形圆心之间的距离是否小于两个圆形的半径之和。
1
2
3
4
5
6
7
| const isCollided = (sprite, detectSprite) => {
const distance = Math.sqrt(
Math.pow(detectSprite.x - sprite.x, 2),
Math.pow(detectSprite.y - sprite.y, 2),
);
return distance < sprite.radius + detectSprite.radius;
}
|
矩形与圆形的碰撞检测
对于矩形与圆形的碰撞,就是判断矩形的边上最近一点与圆心的距离是否小于半径。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| const isCollided = (rect, circle) => {
const bounding = { x: rect.left, y: rect.top };
if (circle.x < rect.left) {
bounding.x = rect.left;
} else if (circle.x < rect.left + rect.width) {
bounding.x = circle.x;
} else {
bounding.x = rect.left + rect.width;
}
if (circle.y < rect.top) {
bounding.y = rect.top;
} else if (circle.y < rect.top + rect.height) {
bounding.y = circle.y;
} else {
bounding.y = rect.top + rect.height;
}
const distance = Math.sqrt(
Math.pow(bounding.x - circle.x, 2),
Math.pow(bounding.y - circle.y, 2),
);
return distance < circle.radius;
}
|
光线投射法
光线投射法 (Ray Casting):画一条与物体的速度向量相重合的线,然后再从另外一个待检测物体出发,绘制第二条线,根据两条线的交点位置来判定是否发生碰撞。
如果满足如下两个条件,表明发生碰撞:
- 第一条线与第二条线的交点在某个范围内(规定的边界)
- 物体在位于第二条线的下方位置
利用直线的斜截式方程,其中 k 是直线的斜率,b 是直线在 y 轴上的截距,也是直线与 y 轴的交点作纵坐标。
找到这两条线的交点,也就是寻找一个同时满足这两个直线方程式的点,所以可以设 第一条线 等于 第二条线的 方程式(此时两个直线方程中的 x 是相同的),然后解出 x 。
当两条直线存在交点 (x, y) 时,则可以得到如下等式,
需要注意的是,该方法完全忽略了物体做水平运动与垂直运动的情况。在物体做水平运动时,代表物体运动向量的那条线,斜率为 0 ,物体做垂直运动时,运动向量的斜率为 ∞ 无穷大,这两个值都不适合用于该方法所要采用的光线投射法。通常管线投射法都会结合边界值检测来进行严格准确的判断。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| function ballInBucket(ball, bucket) {
const x1 = lastBallPosition.x,
y1 = lastBallPosition.y,
x2 = ball.x,
y2 = ball.y,
x3 = bucket.x + bucket.width / 4,
y3 = bucket.y,
x4 = bucket.x + bucket.width,
y4 = y3,
k1 = (ball.y - lastBallPosition.y) / (ball.x - lastBallPosition.x),
k2 = (y4 - y3) / (x4 - x3),
b1 = y1 - k1 * x1,
b2 = y3 - k2 * x3;
this.intersectionPoint.x = (b2 - b1) / (k1 - k2);
this.intersectionPoint.y = k1 * this.intersectionPoint.x + b1;
return (
this.intersectionPoint.x > x3 &&
this.intersectionPoint.x < x4 &&
ball.x + ball.width < x4 &&
ball.y + ball.height > y3
);
}
|
光线投射检测示例
查看完整 Demo 效果
分离轴定理
分离轴定理(SAT —— Separating Axis Theorem),又叫作 “超平面分离定理”。在前面的几种方式并不适用于任意多边形之间的碰撞检测,分离轴定理可用用来检测不同多边形之间碰撞。分离轴定理只适用于凸多边形,也就是内角和小于 180 度的多边形,凸多边形的各个顶点都是由多边形的中心向外延伸的,如矩形,三角形,正方形。
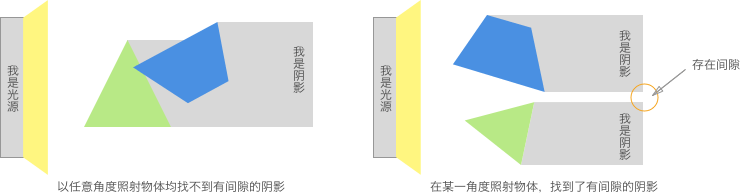
分离轴定理使用数学模型描述:把受测的两个多边形置于一堵墙前面,然后用光线照射它们,然后根据是否相交(是否有间隙)来判断二者有没有相撞。
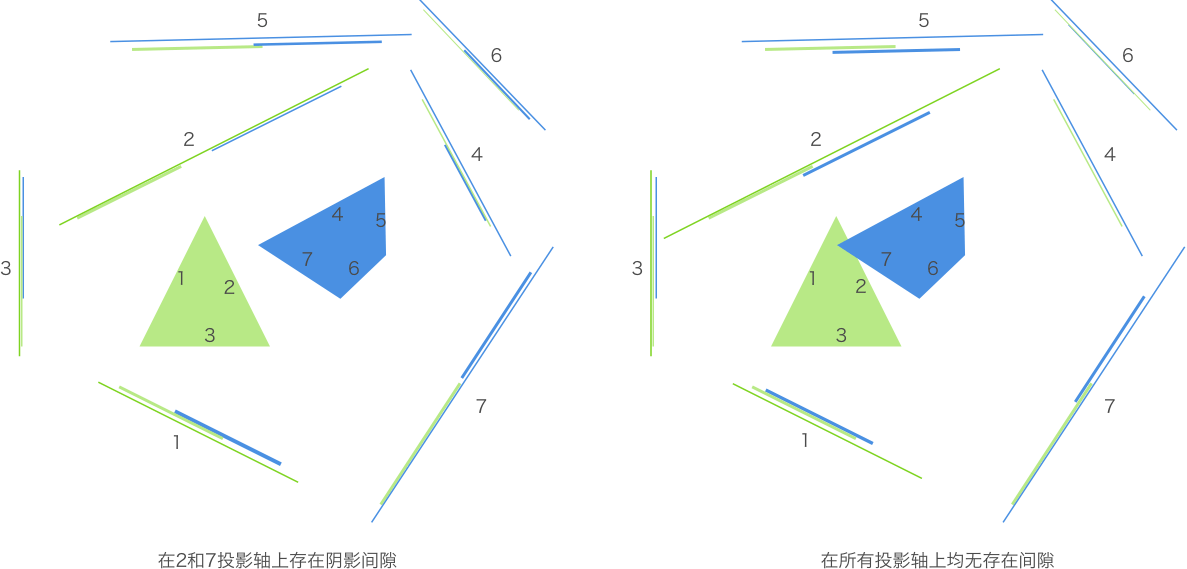
数学的语言叫做 “投影”,那面墙叫做 “轴”,这样用光线从不同的角度照射到两个图形上,这不同角度的一系列阴影投射到它们之后的墙壁上,如果每一个角度上物体的投影没有间隙,那么这两个物体就一定接触到,如果找到了一个间隙,那么说明这两个物体没有接触。简单来说,就是对于两个凸多边形,若存在一条直线将两者分开,则这两个多边形不相交。
实际应用中,遍历所有角度的分离轴是不现实的,计算量会十分密集,幸运的是,由于多边形的性质,只需要检测其中几个关键的角度。对于两个都是多边形的物体,要检测的角度数量就正好是这个多边形的边数,只需要依次在每条边的垂直线做投影即可。如果两个都是矩形则只需要做四次投影。
需要注意的是:分离轴定理只适用于凸多边形的碰撞检测,凸多边形也就是所有内角均小于 180度的多边形,凸多边形的各个定点都是由多边形的中心,向外延伸的,比如巨型,三角形,正方形。如果只有有一个角大于了 180度,那么这个多变从就有了凹陷,就成了凹多边形,不能使用分离轴定理检测凹多边形之间的碰撞。
 投影
投影
 投影轴
投影轴
分离轴检测步骤:
- 先获取被检测多边形的所有的投影轴,一般只需要计算出多边形对应边的投影轴即可
- 计算出被检测多边形在每一条投影轴上的投影
- 判断它们的投影是否有重叠,如果存在在任意一条投影轴的投影不重叠,则说明它们没有发生碰撞,否则就发生了碰撞
使用分离轴定理判断连个多边形是否碰撞,伪代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
| const isCollided = (polygon1, polygon2) => {
const axes = polygon1.getAxes();
axes.push(...polygon2.getAxes());
for(const axis in axes) {
const projection1 = polygon1.projection(axis);
const projection2 = polygon2.projection(axis);
if (!projection1.overlaps(projection2)) {
return false;
}
}
return true;
}
|
将伪代码转换为实际应用之前,需要解决几个问题:
- 如何确定多边形的各个投影轴 ?
- 如何将多边形投射到某条分离轴上 ?
- 如何检测两段投影是否发生重叠 ?
投影轴
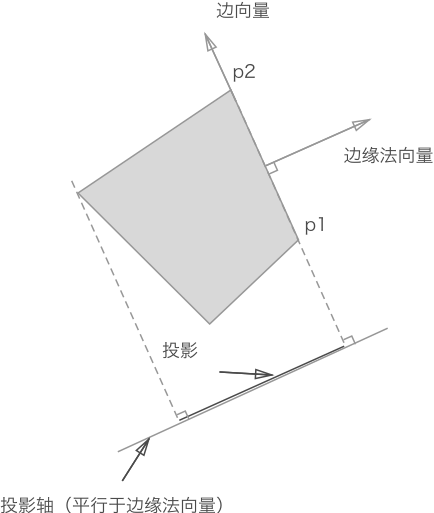
使用分离轴检测多边形的碰撞,必须要能够根据多边形找到它所有的投影轴。如图所示,从 p1 指向 p2 的向量表示多边形的某个边,这个向量叫做边缘向量。还需要确定一条垂直于边缘向量的法向量,叫做边缘法向量。投影轴位于图形下方,但是其实这条轴的位置无所谓,因为这条轴无论位于哪里,轴的是长度无限的,故而多边形在该轴上的投影也都是一样的,这条轴的方向才是关键。
 投影
投影
给定 p1 和 p2 两点,可以得到一条垂直于边缘向量的投影轴。
1
2
3
| const v1 = Vector(p1.x, p1.y);
const v2 = Vector(p2.x, p2.y);
const axis = v1.edge(v2).normal();
|
Vector 的实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
| export class Vector {
public x: number;
public y: number;
public constructor(x?: number, y?: number) {
this.x = x || 0;
this.y = y || 0;
}
public static fromPoint(p: Point) {
return new Vector(p.x, p.y);
}
public equals(v: Vector) {
return this.x === v.x && this.y === v.y;
}
public getMagnitude() {
return Math.sqrt(Math.pow(this.x, 2) + Math.pow(this.y, 2));
}
public add(v: Vector) {
return new Vector(this.x + v.x, this.y + v.y);
}
public subtract(v: Vector) {
return new Vector(this.x - v.x, this.y - v.y);
}
public dotProduct(v: Vector) {
return this.x * v.x + this.y * v.y;
}
public edge(v: Vector) {
return this.subtract(v);
}
public perpendicular() {
return new Vector(this.y, 0 - this.x);
}
public normalize() {
const m = this.getMagnitude();
return new Vector(this.x / m, this.y / m);
}
public normal() {
const p = this.perpendicular();
return p.normalize();
}
public reflect(axis: Vector) {
const vdotl = this.dotProduct(axis);
const ldotl = axis.dotProduct(axis);
const dotProductRatio = vdotl / ldotl;
return new Vector(2 * dotProductRatio * axis.x - this.x, 2 * dotProductRatio * axis.y - this.y);
}
}
|
perpendicular() 获取与之垂直的向量, normalize() 获取归一化后的向量。现在只需要把需要检测的多边形的每一条边所对应的投影轴确定下来,并检测每条轴上的投影是否有分离。有分离则未碰撞,否则则碰撞。
Projection 类检测是否发生重叠:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| export class Projection {
public min: number;
public max: number;
public constructor(min: number, max: number) {
this.min = min;
this.max = max;
}
public overlaps(p: Projection) {
return this.max > p.min && p.max > this.min;
}
public getOverlap(projection: Projection) {
if (!this.overlaps(projection)) {
return 0;
}
let overlap;
if (this.max > projection.max) {
overlap = projection.max - this.min;
} else {
overlap = this.max - projection.min;
}
return overlap;
}
}
|
Polygon 类的 getAxes() 方法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
export class Polygon extends Shape {
public points: Point[] = [];
public getAxes(): Vector[] {
const axes = [];
const len = this.points.length;
for (let i = 0; i < len - 1; i++) {
const p1 = this.points[i];
const p2 = this.points[i + 1];
const v1 = new Vector(p1.x, p1.y);
const v2 = new Vector(p2.x, p2.y);
axes.push(v1.edge(v2).normal());
}
const v1 = new Vector(this.points[len - 1].x, this.points[len - 1].y);
const v2 = new Vector(this.points[0].x, this.points[0].y);
axes.push(v1.edge(v2).normal());
return axes;
}
}
|
Shape 类的检测是否碰撞
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| export abstract class Shape {
public collidesWith(shape: Shape) {
const axes = this.getAxes().concat(shape.getAxes());
return !this.separationOnAxes(axes, shape);
}
public separationOnAxes(axes: Array<Vector>, shape: Shape) {
for (let i = 0, len = axes.length; i < len; i++) {
const axis = axes[i];
const projection1 = shape.project(axis);
const projection2 = this.project(axis);
if (!projection1.overlaps(projection2)) {
return true;
}
}
return false;
}
public abstract move(dx: number, dy: number): void;
public abstract createPath(context: CanvasRenderingContext2D): void;
public abstract getAxes(): Vector[];
public abstract project(axis: Vector): Projection;
public abstract centroid(): Point;
public abstract getBoundingBox(): Rectangle;
public abstract collidesMTVWith(shape: Shape, displacement?: number): MinimumTranslationVector;
}
|
分离轴定理碰撞检测示例
查看完整 Demo 效果